Difference between revisions of "DPL94 math"
(Added a see also section and category link to shift the page out of the Special:UncategorizedPages list.) |
(→Figure: Switched to labelled section transclusions for the citation.) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __TOC__ | ||
| + | |||
== Equation == | == Equation == | ||
<math> | <math> | ||
| Line 4: | Line 6: | ||
</math> | </math> | ||
| − | Expressing in terms of | + | Expressing in terms of {{:omega1}}, {{:omegaeff}} <br> |
<math> | <math> | ||
\sin^2\theta \left( \frac{\Phi_\textrm{ex} \textrm{k}_\textrm{ex}}{\textrm{k}_\textrm{ex}^2 + \omega_\textrm{e}^2} \right) = | \sin^2\theta \left( \frac{\Phi_\textrm{ex} \textrm{k}_\textrm{ex}}{\textrm{k}_\textrm{ex}^2 + \omega_\textrm{e}^2} \right) = | ||
| Line 57: | Line 59: | ||
== Figure == | == Figure == | ||
| − | See Figure 1 and 10 in the reference | + | See Figure 1 and 10 in the reference: |
| − | + | ||
| + | * {{#lst:Citations|PalmerMassi06}} | ||
[[File:Fig1 Palmer Massi 2006.png|thumb|center|upright=3|Try to reproduce Figure 1.]] | [[File:Fig1 Palmer Massi 2006.png|thumb|center|upright=3|Try to reproduce Figure 1.]] | ||
Latest revision as of 16:00, 6 November 2015
Contents
Equation
[math] \mathrm{R}_{1\rho}= \mathrm{R}_1\cos^2\theta + \left( \mathrm{R}_{1\rho}{´} + \frac{\Phi_\textrm{ex} \textrm{k}_\textrm{ex}}{\textrm{k}_\textrm{ex}^2 + \omega_\textrm{e}^2} \right) \sin^2\theta [/math]
Expressing in terms of ω1, ωe
[math]
\sin^2\theta \left( \frac{\Phi_\textrm{ex} \textrm{k}_\textrm{ex}}{\textrm{k}_\textrm{ex}^2 + \omega_\textrm{e}^2} \right) =
\frac{w_\textrm{1}^2}{w_\textrm{eff}^2} \cdot \left( \frac{\Phi_\textrm{ex} \textrm{k}_\textrm{ex}}{\textrm{k}_\textrm{ex}^2 + w_\textrm{1}^2 + \Omega^2} \right) =
\frac{w_\textrm{1}^2}{w_\textrm{1}^2 + \Omega^2} \cdot \left( \frac{\Phi_\textrm{ex} \textrm{k}_\textrm{ex}}{\textrm{k}_\textrm{ex}^2 + w_\textrm{1}^2 + \Omega^2} \right)
[/math]
Ramp code
import matplotlib.pyplot as plt
import numpy as np
from math import atan2
phi = 2.0
kex = 3.0
def calc(w1_arr, Omega_arr, p, k):
val_arr = []
for w1 in w1_arr:
for Omega in Omega_arr:
theta = atan2(w1 , Omega)
val = w1**2/(w1**2+Omega**2) * (p*k/(k**2 + w1**2 + Omega**2))
#val = (p*k/(k**2 + w1**2 + Omega**2))
val_arr.append([w1, Omega, theta, val])
return np.array(val_arr)
w1 = np.arange(0., 20, 1)
Omega = np.array([5])
data = calc(w1, Omega, phi, kex)
plt.figure(1)
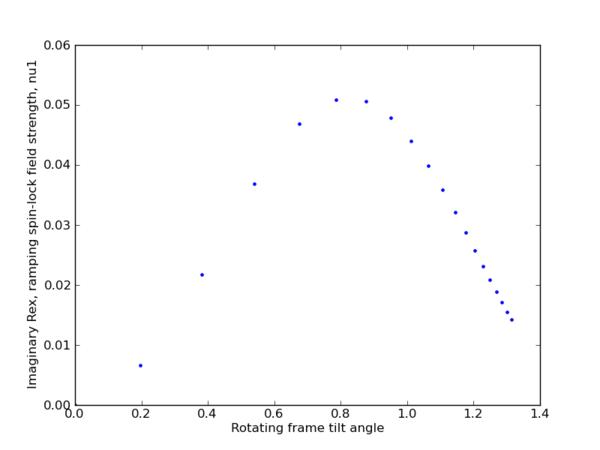
plt.plot(data[:,2], data[:,3], '.')
plt.ylabel(r'Imaginary Rex, ramping spin-lock field strength, nu1')
plt.xlabel(r'Rotating frame tilt angle')
Omega = np.arange(0., 20, 1)
w1 = np.array([5])
data = calc(w1, Omega, phi, kex)
plt.figure(2)
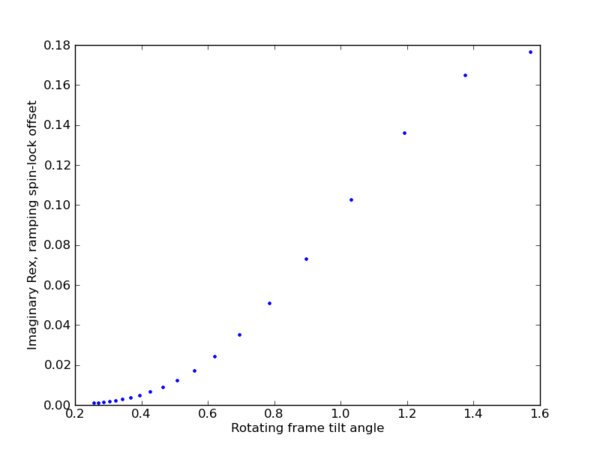
plt.plot(data[:,2], data[:,3], '.')
plt.ylabel(r'Imaginary Rex, ramping spin-lock offset')
plt.xlabel(r'Rotating frame tilt angle')
plt.show()
Ramping
Figure
See Figure 1 and 10 in the reference:
- Palmer, 3rd, A. G. and Massi, F. (2006). Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem. Rev., 106(5), 1700-1719. (DOI: 10.1021/cr0404287)
Figure produced with script found here.