Difference between revisions of "B14"
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | The Baldwin 2014 2-site exact solution relaxation dispersion model for [[SQ CPMG-type data]] for all time scales whereby the simplification {{:R2Azero}} = {{:R2Bzero}} is assumed. This model is labelled as '''B14''' in [[Relaxation dispersion citation for relax|relax]]. | |
| − | |||
| − | The Baldwin 2014 2-site exact solution relaxation dispersion model for [[SQ CPMG-type data]] for all time scales whereby the simplification | ||
The advantage of this code will be that you'll always get the right answer provided you've got 2-site exchange, in-phase magnetisation and on-resonance pulses. | The advantage of this code will be that you'll always get the right answer provided you've got 2-site exchange, in-phase magnetisation and on-resonance pulses. | ||
| − | = Comments from the Author = | + | == Comments from the Author == |
During the implementation of model B14, Andrew Baldwin wished to raise the attention to: | During the implementation of model B14, Andrew Baldwin wished to raise the attention to: | ||
| − | '''1) Danger of errors of approximations'''. | + | '''1) Danger of errors of approximations'''.<br> |
'''2) That optimal accuracy analysis should include off resonance effects'''. | '''2) That optimal accuracy analysis should include off resonance effects'''. | ||
Please read: | Please read: | ||
| − | * | + | * {{#lst:Citations|MyintIshima09}} |
| − | * | + | * {{#lst:Citations|Bain11}} |
'''Differential relaxation effects''':<br> | '''Differential relaxation effects''':<br> | ||
Please read: | Please read: | ||
| − | * | + | * {{#lst:Citations|Vallurupalli07}} |
| − | * | + | * {{#lst:Citations|Vallurupalli08}} |
== Equation == | == Equation == | ||
| Line 80: | Line 78: | ||
== Parameters == | == Parameters == | ||
| − | The B14 model has the parameters { | + | The B14 model has the parameters {{{:R2zero}}, ..., {{:pA}}, {{:Deltaomega}}, {{:kex}}}. |
== Code == | == Code == | ||
| Line 87: | Line 85: | ||
[https://gna.org/support/?3154 Here is gna.org tracker that followed this code. It includes valuable comments.] | [https://gna.org/support/?3154 Here is gna.org tracker that followed this code. It includes valuable comments.] | ||
| − | The library code | + | The library code: {{relax url|path=lib/dispersion/b14.py}} |
| − | |||
| − | The target function | + | The target function func_B14(): {{relax url|path=target_functions/relax_disp.py}} |
| − | |||
=== Example graph of test data === | === Example graph of test data === | ||
| Line 100: | Line 96: | ||
The reference for the B14 model is: | The reference for the B14 model is: | ||
| − | * | + | * {{#lst:Citations|Baldwin14}} |
== Related models == | == Related models == | ||
| Line 109: | Line 105: | ||
The [[Relaxation dispersion citation for relax|implementation of the B14 model in relax]] can be seen in the: | The [[Relaxation dispersion citation for relax|implementation of the B14 model in relax]] can be seen in the: | ||
| − | * [http://www.nmr-relax.com/manual/ | + | * [http://www.nmr-relax.com/manual/The_reduced_B14_2_site_CPMG_model.html relax manual], |
* [http://www.nmr-relax.com/api/3.1/lib.dispersion.b14-module.html API documentation], | * [http://www.nmr-relax.com/api/3.1/lib.dispersion.b14-module.html API documentation], | ||
* [http://www.nmr-relax.com/analyses/relaxation_dispersion.html#B14 relaxation dispersion page of the relax website]. | * [http://www.nmr-relax.com/analyses/relaxation_dispersion.html#B14 relaxation dispersion page of the relax website]. | ||
== See also == | == See also == | ||
| − | [[Category:Relaxation_dispersion]] | + | [[Category:Models]] |
| + | [[Category:Dispersion models]] | ||
| + | [[Category:Relaxation_dispersion analysis]] | ||
Latest revision as of 12:16, 27 October 2017
The Baldwin 2014 2-site exact solution relaxation dispersion model for SQ CPMG-type data for all time scales whereby the simplification R2A0 = R2B0 is assumed. This model is labelled as B14 in relax.
The advantage of this code will be that you'll always get the right answer provided you've got 2-site exchange, in-phase magnetisation and on-resonance pulses.
Contents
Comments from the Author
During the implementation of model B14, Andrew Baldwin wished to raise the attention to:
1) Danger of errors of approximations.
2) That optimal accuracy analysis should include off resonance effects.
Please read:
- Myint, W. and Ishima, R. (2009). Chemical exchange effects during refocusing pulses in constant-time CPMG relaxation dispersion experiments J. Biomol. NMR, 45(1), 207-216. (DOI: 10.1007/s10858-009-9344-9)
- Bain, A. D., Anand, C. A., and Nie, Z. (2011). Exact solution of the CPMG pulse sequence with phase variation down the echo train: Application to R2 measurements J. Magn. Reson., 209(2), 183-194. (DOI: 10.1016/j.jmr.2011.01.009)
Differential relaxation effects:
Please read:
- Vallurupalli, P., Hansen, D. F., Stollar, E., Meirovitch, E. and Kay, L. E. (2007). Measurement of bond vector orientations in invisible excited states of proteins Proc. Natl. Acad. Sci. USA, 104(47), 18473-18477. (DOI: 10.1073/pnas.0708296104)
- Vallurupalli, P., Hansen, D. F., and Kay, L. E. (2008). Structures of invisible, excited protein states by relaxation dispersion NMR spectroscopy Proc. Natl. Acad. Sci. USA, 105(33), 11766-11771. (DOI: 10.1073/pnas.0804221105)
Equation
The paper main equation 50
[math]
R_{2,\textrm{eff}} = \frac{R_2^A+R_2^B+k_{\textrm{EX}}}{2}-\frac{N_{\textrm{CYC}}}{T_{\textrm{rel}}}\cosh{}^{-1}(v_{1c}) - \frac{1}{T_{\textrm{rel}}}\ln{\left( \frac{1+y}{2} + \frac{1-y}{2\sqrt{v_{1c}^2-1}}(v_2 + 2k_{\textrm{AB}}p_D )\right)} \\
= R_{2,\textrm{eff}}^{\textrm{CR72}} - \frac{1}{T_{\textrm{rel}}}\ln{\left( \frac{1+y}{2} + \frac{1-y}{2\sqrt{v_{1c}^2-1}}(v_2 + 2k_{\textrm{AB}}p_D )\right)}
[/math]
Which have these following definitions
[math]
v_{1c} = F_0\cosh{\left(\tau_{\textrm{CP}}E_0\right)}-F_2\cosh{\left(\tau_{\textrm{CP}}E_2\right)} \\
v_{1s} = F_0\sinh{\left(\tau_{\textrm{CP}}E_0\right)}-F_2\sinh{\left(\tau_{\textrm{CP}}E_2\right)} \\
v_{2}N = v_{1s}\left(O_B-O_A\right)+4O_B F_1^a \sinh{\left(\tau_{\textrm{CP}}E_1\right)} \\
p_D N = v_{1s} + \left(F_1^a+F_1^b\right)\sinh{\left(\tau_{\textrm{CP}}E_1\right)}\\
v_3 = \left( v_2^2 + 4 k_{\textrm{BA}} k_{\textrm{AB}} p_D^2 \right)^{1/2} \\
y = \left( \frac{v_{1c}-v_3}{v_{1c}+v_3} \right)^{N_{\textrm{CYC}}}
[/math]
Note, [math] E_2 [/math] is complex. If |x| denotes the complex modulus:
[math]
\cosh{\left(\tau_{\textrm{CP}}E_2\right)} = \cos{\left(\tau_{\textrm{CP}}|E_2|\right)} \\
\sinh{\left(\tau_{\textrm{CP}}E_2\right)} = i \sin{\left(\tau_{\textrm{CP}}|E_2|\right)}
[/math]
The term [math]p_D[/math] is based on product of the off diagonal elements in the CPMG propagator (Supplementary Section 3).
It is interesting to consider the region of validity of the Carver Richards result. The two results are equal when the correction is zero, which is true when
[math]
\sqrt{v_{1c}^2-1} \approx v_2 + 2k_{\textrm{AB}}p_D
[/math]
This occurs when [math]k_{\textrm{AB}}p_D[/math] tends to zero, and so [math]v_2=v_3[/math].
Setting [math]k_{\textrm{AB}}p_D[/math] to zero, amounts to neglecting magnetisation that starts on the ground state ensemble and end on the excited state ensemble and vice versa.
This will be a good approximation when [math]p_A \gg p_B[/math].
In practise, significant deviations from the Carver Richards equation can be incurred if [math]p_B \gt 1\%[/math].
Incorporation of the correction term into equation (50), results in an improved description of the CPMG experiment over the Carver Richards equation.
Equation compared to Carver Richards 72
Please see the relax summary of the model parameters here.
These definitions comes from the papers "Supplementary Section 4. Relation to Carver Richards equation".
[math] \tau_{\textrm{CP}} = \frac{1}{4\nu_\textrm{CPMG}} \\ \alpha_- = k_{\textrm{AB}} - k_{\textrm{BA}} \\ \zeta = 2 \Delta \omega \, \alpha_- = h_1\\ \Psi = \alpha_-^2 + 4 k_{\textrm{BA}} k_{\textrm{AB}} - \Delta \omega^2 = h_2\\ \xi = \frac{2\tau_{\textrm{CP}}}{\sqrt{2}}\sqrt{\Psi + \sqrt{\Psi^2 + \zeta^2}} = 2h_3 \tau_{\textrm{CP}} = \tau_{\textrm{CP}}E_0\\ \eta = \frac{2\tau_{\textrm{CP}}}{\sqrt{2}}\sqrt{-\Psi + \sqrt{\Psi^2 + \zeta^2}} = 2h_4 \tau_{\textrm{CP}} = \tau_{\textrm{CP}}E_2\\ D_+=\frac{1}{2}\left(1+\frac{\Psi+2\Delta \omega^2}{\sqrt{\Psi^2+\zeta^2}} \right) = F_0 \\ D_-=\frac{1}{2}\left(-1+\frac{\Psi+2\Delta \omega^2}{\sqrt{\Psi^2+\zeta^2}} \right) = F_2 [/math]
Physical meanings:
[math]\xi[/math] and [math]\eta[/math] are differences of the real and imaginary components of the free precession frequencies [math]f_{00}[/math] and [math]f_{11}[/math] (equation (41)).
[math]D_+[/math] and [math]D_-[/math] are the stay/stay ([math]F_{0}[/math]), and swap/swap ([math]F_{2}[/math]) coefficients (equation (36)).
[math]\zeta[/math] and [math]\Psi[/math] are parameters that enable the free precession frequencies to be written in a more concise form (equation (12)).
Note that in reference 2 (10.1016/S0076-6879(01)39315-1), in equation 25, the definition used for [math]\tau_{\textrm{CP}}[/math] is twice that used in this work but is otherwise identical.
Parameters
The B14 model has the parameters {R20, ..., pA, Δω, kex}.
Code
Commits that created the code, approx 20-30 commits, with corrections.
Here is gna.org tracker that followed this code. It includes valuable comments.
The library code: https://sourceforge.net/p/nmr-relax/code/ci/master/tree/lib/dispersion/b14.py
The target function func_B14(): https://sourceforge.net/p/nmr-relax/code/ci/master/tree/target_functions/relax_disp.py
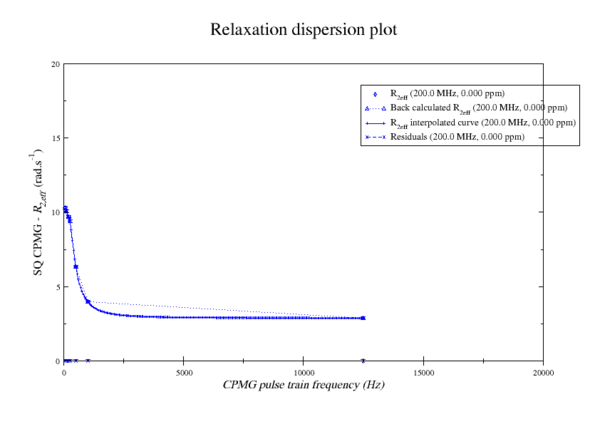
Example graph of test data
Reference
The reference for the B14 model is:
- Baldwin A. J. (2014). An exact solution for R2,eff in CPMG experiments in the case of two site chemical exchange. J. Magn. Reson., 244, 114-124. (DOI: 10.1016/j.jmr.2014.02.023)
Related models
The B14 model is a linear correction to the CR72 model, and algorithms based on this have significant advantages in both precision and speed over existing formulaic approaches.
Links
The implementation of the B14 model in relax can be seen in the: