relax disp.spin lock offset+field
Contents
Setting up relax_disp.spin_lock_offset and relax_disp.spin_lock_field
Refer to the manual for parameter explanation
This page is a little help to understand how to use the functions:
- relax_disp.spin_lock_offset()
- relax_disp.spin_lock_field()
spin lock offset
Manual on relax_disp.spin_lock_offset
The relax function relax_disp.spin_lock_offset() requires the values to be provided in ppm.
relax_disp.spin_lock_offset(spectrum_id=None, offset=None)
spin lock field
Manual on relax_disp.spin_lock_field
The relax function relax_disp.spin_lock_field() requires the values to be provided in Hz.
relax_disp.spin_lock_field(spectrum_id=None, field=None)
Literature comments
See Figure 1 and 10 in the reference:
- Palmer, 3rd, A. G. and Massi, F. (2006). Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem. Rev., 106(5), 1700-1719. (DOI: 10.1021/cr0404287)
Figure produced with script found here.
Calculations in relax
spin lock offset
In the literature, the values are often stated as "offset", "carrier offset", "offset of the spin-lock pulse" with values given in Hz, and can have values from 0-500 to 10-20.000 Hz.
These values reflects offset frequencies to the carrier frequency, and in relax is noted as "Spin-lock offset, the frequency of of the rf field" : ωrf.
Relax needs input for ωrf in ppm, and during calculations converts to the rad/s, with the following function call.
offsets[ei][si][mi][oi] = frequency_to_rad_per_s(frq=cdp.spin_lock_offset[id], B0=frq, isotope=spin.isotope)
If you need to convert to ppm from Hz values, consider during this in your relax script.
If for example you have recorded at a 800 MHz spectrometer, you could find the Carrier position for 15N (Value of yCar in NMRPipe scripts). If yCAR = 118.078 ppm, then
from lib.nmr import frequency_to_Hz, frequency_to_ppm
# Spectrometer frequency
sfrq = 799.7773991 # MHz
# Carrier position
yCAR = 118.078 # ppm
# We take the absolute value, since the gyromagnetic ratio of N15 is negative.
yCAR_Hz = abs(frequency_to_Hz(frq=yCAR, B0=sfrq*1E6, isotope='15N'))
# We add the offset (deltadof2 in varian pulse sequences) in Hz, and from 0 to 10.000
yCar_offset_Hz = yCAR_Hz + float(deltadof2)
# The convert back from Hz to ppm. Again absolute value, because of the gyromagnetic ratio of N15 is negative.
yCar_offset_ppm = abs(frequency_to_ppm(frq=yCar_offset_Hz, B0=sfrq*1E6, isotope='15N'))
relax_disp.spin_lock_offset(spectrum_id=sp_id, offset=yCar_offset_ppm)
Offset in the literature
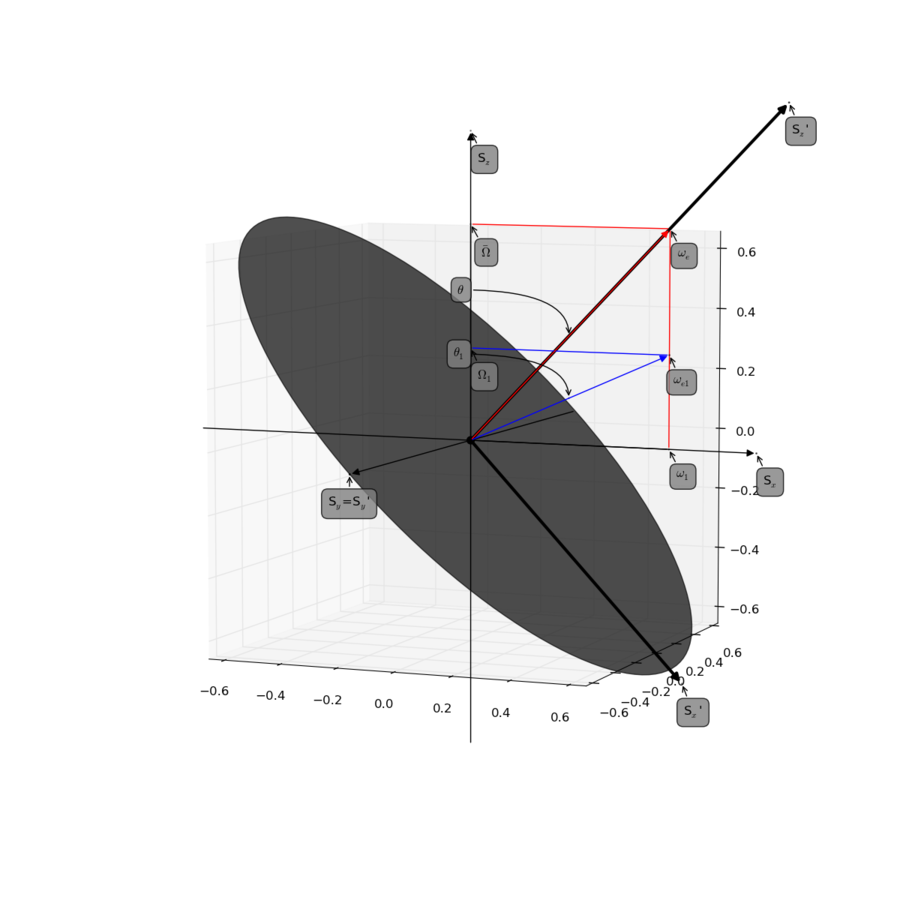
The offset is in the literature noted as ΩS, where ΩS is the (Ex. 15N) resonance offset from the spin-lock carrier.
Note that ΩS is dependent of the chemical shifts δ in ppm for the nuclei of interest.
The Chemical Shifts δ in ppm for nuclei of interest (ex. 15N and which have been loaded in with relax function chemical_shift_read from a peak list formatted file) is first converted to to the rad/s with the following function calls.
[math] \bar{\omega}_{S,i} = 2\pi \cdot \delta_{S,i} \cdot B_0 \cdot \frac{\gamma_{^{15}N}}{\gamma_{^{1}H}} [/math]
shifts[ei][si][mi] = frequency_to_rad_per_s(frq=shift, B0=frq, isotope=spin.isotope)
Then ΩS is calculated with: ΩS,i = ΩS,i - ωrf, where Ω is the population averaged Larmor frequency of the spin and comes from the conversion of the Chemical Shifts δS,i to frequency ΩS,i.
Delta_omega = shifts[ei][si][mi] - offsets[ei][si][mi][oi]
spin lock field
The spin lock field strength is noted ν1, and relax requires these to be provided in unit of rad/s.
The spin lock field strength is converted to rad/s, with the following function call.
[math] \omega_{S,1} = 2\pi \cdot \nu_{S,1} [/math]
omega1 = point * 2.0 * pi
Then the Rotating frame tilt angle θ is calculated.
[math] \theta = \tan^{-1} \left( \frac{\omega_1}{\bar{\Omega}_{S,i}} \right) [/math]
if Delta_omega == 0.0:
theta[ei][si][mi][oi].append(pi / 2.0)
# Calculate the theta angle describing the tilted rotating frame relative to the laboratory.
# If Delta_omega is negative, there follow the symmetry of atan, that atan(-x) = - atan(x).
# Then it should be: theta = pi + atan(-x) = pi - atan(x) = pi - abs(atan( +/- x))
elif omega1 / Delta_omega > 0 :
theta[ei][si][mi][oi].append(atan(omega1 / Delta_omega))
else:
theta[ei][si][mi][oi].append(pi + atan(omega1 / Delta_omega))
Code reference calculations in relax
The code which is called resides in:
lib/nmr.py
frequency_to_rad_per_s(frq=None, B0=None, isotope=None):
"""Convert the given frequency from ppm to rad/s units."""
return frq * 2.0 * pi * B0 / g1H * return_gyromagnetic_ratio(isotope) * 1e-6
specific_analyses/relax_disp/disp_data.py
return_offset_data(spins=None, spin_ids=None, field_count=None, fields=None):
Data structures
"""
The data structures consist of many different index types. These are:
- Ei: The index for each experiment type.
- Si: The index for each spin of the spin cluster.
- Mi: The index for each magnetic field strength.
- Oi: The index for each spin-lock offset.
- Di: The index for each dispersion point, the spin-lock field strength.
"""
Spectrometer notes
Varian / VnmrJ
In some pulse sequences, the following is seen:
'trim' is a basic timeunit and the total spinlock time is calculated as 2.0*ncyc*trim
b1 = getval("b1"), /* spin-lock field, Hz! */
deltadof2 = getval("deltadof2"), /* offset for N15 spinlock */