Relax disp.spin lock offset+field

Setting up relax_disp.spin_lock_offset and relax_disp.spin_lock_field

Refer to the manual for parameter explanation

This page is a little help to understand how to use the functions:

1. relax_disp.spin_lock_offset()
2. relax_disp.spin_lock_field()

spin lock offset

Manual on relax_disp.spin_lock_offset
The relax function relax_disp.spin_lock_offset() requires the values to be provided in ppm.

relax_disp.spin_lock_offset(spectrum_id=None, offset=None)

spin lock field

Manual on relax_disp.spin_lock_field
The relax function relax_disp.spin_lock_field() requires the values to be provided in Hz.

relax_disp.spin_lock_field(spectrum_id=None, field=None)

Literature comments

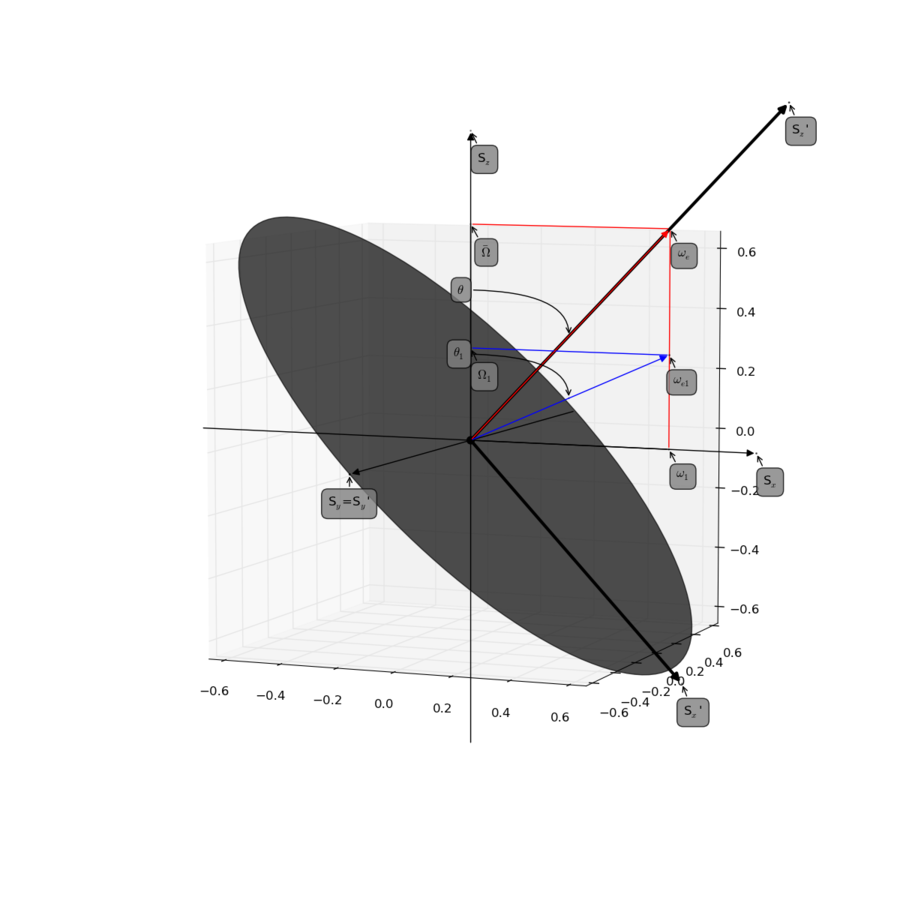
See Figure 1 and 10 in the reference.

Palmer, A.G. & Massi, F. (2006). Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem. Rev. 106, 1700-1719 DOI

Try to reproduce Figure 1.

Figure produced with script found here.

Calculations in relax

spin lock offset

In the literature, the values are often stated as "offset", "carrier offset", "offset of the spin-lock pulse" with values given in Hz, and can have values from 0-500 to 10-20.000 Hz.
These values reflects offset frequencies to the carrier frequency, and in relax is noted as "Spin-lock offset, the frequency of of the rf field" : $\mathbf{\omega_{rf}}$.

Relax needs input for $\mathbf{\omega_{rf}}$ in ppm, and during calculations converts to the rad/s, with the following function call.

offsets[ei][si][mi][oi] = frequency_to_rad_per_s(frq=cdp.spin_lock_offset[id], B0=frq, isotope=spin.isotope)

Offset in the literature

The offset is in the literature noted as $\Omega_S$, where $\Omega_S$ is the (Ex. $^{15}$N) resonance offset from the spin-lock carrier.

Note that $\Omega_S$ is dependent of the chemical shifts $\delta$ in ppm for the nuclei of interest.

The Chemical Shifts $\delta$ in ppm for nuclei of interest (ex. $^{15}$N and which have been loaded in with relax function chemical_shift_read from a peak list formatted file) is first converted to to the rad/s with the following function calls.
$\bar{\omega}_{S,i} = 2\pi \cdot \delta_{S,i} \cdot B_0 \cdot \frac{\gamma_{^{15}N}}{\gamma_{^{1}H}}$

shifts[ei][si][mi] = frequency_to_rad_per_s(frq=shift, B0=frq, isotope=spin.isotope)

Then $\bar{\Omega}_S$ is calculated with: $\bar{\Omega}_{S,i} = \bar{\omega}_{S,i} - \omega_{rf}$, where $\bar{\omega}$ is the population averaged Larmor frequency of the spin and comes from the conversion of the Chemical Shifts $\delta_{S,i}$ to frequency $\bar{\omega}_{S,i}$.

Delta_omega = shifts[ei][si][mi] - offsets[ei][si][mi][oi]

spin lock field

The spin lock field strength is noted $\nu_1$, and relax requires these to be provided in unit of Hz.

The spin lock field strength is converted to rad/s, with the following function call.
$\omega_{S,1} = 2\pi \cdot \nu_{S,1}$

omega1 = point * 2.0 * pi

Then the Rotating frame tilt angle $\theta$ is calculated.
$\theta = \tan^{-1} \left( \frac{\omega_1}{\bar{\Omega}_{S,i}} \right)$

if Delta_omega == 0.0:
    theta[ei][si][mi][oi].append(pi / 2.0)
# Calculate the theta angle describing the tilted rotating frame relative to the laboratory.
# If Delta_omega is negative, there follow the symmetry of atan, that atan(-x) = - atan(x).
# Then it should be: theta = pi + atan(-x) = pi - atan(x) = pi - abs(atan( +/- x))
elif omega1 / Delta_omega > 0 :
    theta[ei][si][mi][oi].append(atan(omega1 / Delta_omega))
else:
    theta[ei][si][mi][oi].append(pi + atan(omega1 / Delta_omega))

Code reference calculations in relax

The code which is called resides in:

lib/nmr.py

frequency_to_rad_per_s(frq=None, B0=None, isotope=None):

"""Convert the given frequency from ppm to rad/s units."""
return frq * 2.0 * pi * B0 / g1H * return_gyromagnetic_ratio(isotope) * 1e-6

specific_analyses/relax_disp/disp_data.py

return_offset_data(spins=None, spin_ids=None, field_count=None, fields=None):

Data structures

"""
The data structures consist of many different index types.  These are:

- Ei:  The index for each experiment type.
- Si:  The index for each spin of the spin cluster.
- Mi:  The index for each magnetic field strength.
- Oi:  The index for each spin-lock offset.
- Di:  The index for each dispersion point, the spin-lock field strength.
"""

Spectrometer notes

Varian / VnmrJ

In some pulse sequences, the following is seen:

'trim' is a basic timeunit and the total spinlock time is calculated as 2.0*ncyc*trim
b1 = getval("b1"),                      /* spin-lock field, Hz! */  
deltadof2 = getval("deltadof2"),        /* offset for N15 spinlock */